

Next: Fit QA
Up: Fitting of histograms
Previous: The fit function
The main objective of the fit-procedure is to use Eq. 2
to fit the 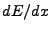 distributions in every phase space bin. The full
function has 12 parameters (5 amplitudes, 5 positions, width and
asymmetry). It is practically impossible to fit all these parameters
in every bin. However, some of the parameters are likely to be
distributions in every phase space bin. The full
function has 12 parameters (5 amplitudes, 5 positions, width and
asymmetry). It is practically impossible to fit all these parameters
in every bin. However, some of the parameters are likely to be
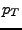 -independent. In the fit, it is assumed that all the relative
-independent. In the fit, it is assumed that all the relative
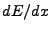 peak positions (
peak positions (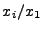 ) are pt-independent. The electron and
deuteron relative positions are fixed to a paremeterisation of the
peak positions as function of
) are pt-independent. The electron and
deuteron relative positions are fixed to a paremeterisation of the
peak positions as function of 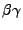 . This parameterisation was
obtained from fits to some of the bins with larger statistics. The
parameterisation is as follows:
. This parameterisation was
obtained from fits to some of the bins with larger statistics. The
parameterisation is as follows:
![\begin{displaymath}
\left\langle\frac{dE}{dx}\right\rangle=A\frac{B}{\beta^2}\left[\ln \frac{\beta^2}{1-\beta^2}-\beta^2-\delta(\beta)\right],
\end{displaymath}](img35.png) |
(3) |
where the first two terms are the original Bethe-Bloch formula. The
factors 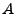 and
and 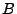 are given in the Bethe-Bloch formula in terms of
the ionisation energy of the medium and some fundamental constants,
but for our fits we determine them from the data. The
third term limits the energy loss to finite values in the
logarithmic-rise region. It is calculated as follows:
are given in the Bethe-Bloch formula in terms of
the ionisation energy of the medium and some fundamental constants,
but for our fits we determine them from the data. The
third term limits the energy loss to finite values in the
logarithmic-rise region. It is calculated as follows:
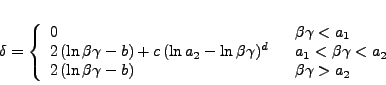 |
(4) |
The values of 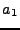 and
and 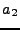 are calculated by requiring continuity
of the term
are calculated by requiring continuity
of the term 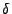 . The constanst
. The constanst 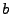 ,
, 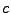 and
and 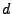 are specific to
the medium and are tabulated for some gases and solid. In NA49,
are specific to
the medium and are tabulated for some gases and solid. In NA49, 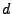 is
set to 3, and the other two constants are fitted to the data. The
full equation is quite complicated, but it is implemented in T49SumGaus::RelRise and T49SumGaus::GetRelRise for easy
use. The various constants in the implemented function can be set
using T49SumGaus::SetBBPars . In the final version of the fit-macro,
the constants are set to T49SumGaus::SetBBPars(1.613702, 10.407406, 2.463701, 0.164279) .
is
set to 3, and the other two constants are fitted to the data. The
full equation is quite complicated, but it is implemented in T49SumGaus::RelRise and T49SumGaus::GetRelRise for easy
use. The various constants in the implemented function can be set
using T49SumGaus::SetBBPars . In the final version of the fit-macro,
the constants are set to T49SumGaus::SetBBPars(1.613702, 10.407406, 2.463701, 0.164279) .
This parametrisation is then used to fix the peak positions of the
electrons and deuterons in the fits. The kaon and proton relative
positions are determined from a simultaneous fit to all 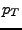 bins at
each
bins at
each 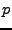 . The same is done for the asymmetry parameter
. The same is done for the asymmetry parameter 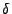 . The
remaining parameters are 7 per phase space bin (5 amplitudes, pion
peak position and resolution). The deuteron peak amplitude is set to 0
for all bins at negative charge. In addition, the peak amplitudes are
constrained to be 0 or larger. For technical reasons, if one of the
peak amplitudes ends up at 0 from the free fit, it is fixed to 0 and a
refit is done for a better evaluation of the errors and better
stability of the simultaneous fit. The fit is carried out by the macro
fit_ptb_asym_chisq_deut.C . This macro uses a
. The
remaining parameters are 7 per phase space bin (5 amplitudes, pion
peak position and resolution). The deuteron peak amplitude is set to 0
for all bins at negative charge. In addition, the peak amplitudes are
constrained to be 0 or larger. For technical reasons, if one of the
peak amplitudes ends up at 0 from the free fit, it is fixed to 0 and a
refit is done for a better evaluation of the errors and better
stability of the simultaneous fit. The fit is carried out by the macro
fit_ptb_asym_chisq_deut.C . This macro uses a
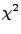 -criterium for minimisation. I have experimented with a
log-likelihood fit, but did not manage to get those to converge
properly.
-criterium for minimisation. I have experimented with a
log-likelihood fit, but did not manage to get those to converge
properly.


Next: Fit QA
Up: Fitting of histograms
Previous: The fit function
Marco van Leeuwen
2009-01-14
![]() bins at
each
bins at
each ![]() . The same is done for the asymmetry parameter
. The same is done for the asymmetry parameter ![]() . The
remaining parameters are 7 per phase space bin (5 amplitudes, pion
peak position and resolution). The deuteron peak amplitude is set to 0
for all bins at negative charge. In addition, the peak amplitudes are
constrained to be 0 or larger. For technical reasons, if one of the
peak amplitudes ends up at 0 from the free fit, it is fixed to 0 and a
refit is done for a better evaluation of the errors and better
stability of the simultaneous fit. The fit is carried out by the macro
fit_ptb_asym_chisq_deut.C . This macro uses a
. The
remaining parameters are 7 per phase space bin (5 amplitudes, pion
peak position and resolution). The deuteron peak amplitude is set to 0
for all bins at negative charge. In addition, the peak amplitudes are
constrained to be 0 or larger. For technical reasons, if one of the
peak amplitudes ends up at 0 from the free fit, it is fixed to 0 and a
refit is done for a better evaluation of the errors and better
stability of the simultaneous fit. The fit is carried out by the macro
fit_ptb_asym_chisq_deut.C . This macro uses a
![]() -criterium for minimisation. I have experimented with a
log-likelihood fit, but did not manage to get those to converge
properly.
-criterium for minimisation. I have experimented with a
log-likelihood fit, but did not manage to get those to converge
properly.